Avaljot Singh

Room 2107
Thomas M Siebel Center
201 Goodwin Avenue
Urbana,
Illinois, 61801
United States
I am a PhD student at the University of Illinois Urbana-Champaign, under the guidance of Prof. Gagandeep Singh and Prof. Charith Mendis. Prior to starting my PhD, I graduated with Bachelors and Masters in Computer Science from IIT Delhi in May 2021, where I was advised by Prof. Sanjiva Prasad (Thesis). I have also had the opportunity of working with Shraddha Barke and Suman Nath at MSR Redmond, Rahul Sharma at MSR India and Prof. Nate Foster at Cornell University during my research internships.
My research is centered on a bidirectional interaction between formal methods and artificial intelligence. On one hand, I develop formal and declarative infrastructures for building trustworthy AI systems using formal methods, with a particular focus on specification, soundness verification, and efficient execution of AI analyses and certification procedures. On the other hand, I study how learning and synthesis techniques can be used to automate and improve formal methods themselves, enabling the automatic construction of verification tools, program analyses, and reasoning procedures. Together, these two directions aim to improve the trustworthiness of AI systems and to substantially reduce the human effort required to build and maintain formal verification frameworks.
Formal Methods for AI
This line of work focuses on building principled and trustworthy AI analysis and certification systems using formal methods. My goal is to make AI analyses and certifiers easier to design, mechanically verifiable for soundness, and efficient to execute, by providing a unified infrastructure that supports specification, formal verification, and compilation of analysis and certification procedures.

ConstraintFlow
ConstraintFlow is a declarative domain-specific language for specifying neural network certifiers and analyses. It provides a compact and modular way to express abstract interpretation-based certifiers, significantly reducing implementation complexity compared to hand-written implementations.
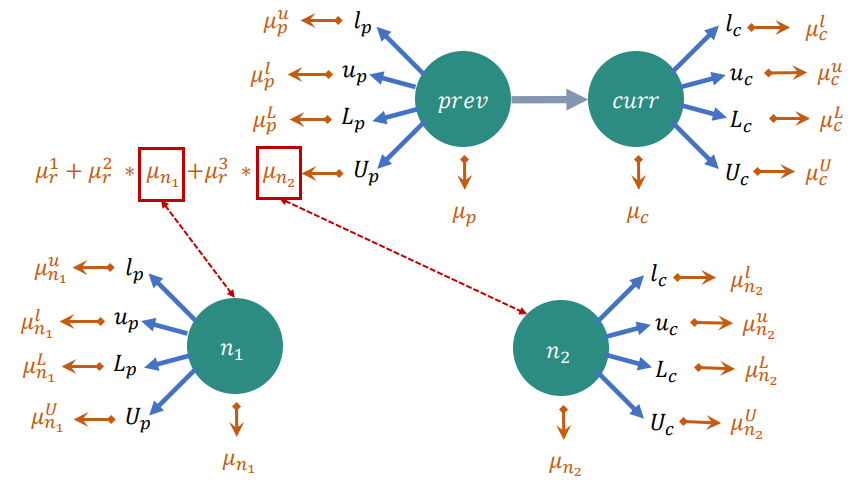
ProveSound
ProveSound automatically verifies the soundness of neural network certifiers written in ConstraintFlow. It checks that a certifier implementation correctly over-approximates the concrete neural network semantics, providing formal guarantees about the correctness of certification algorithms.
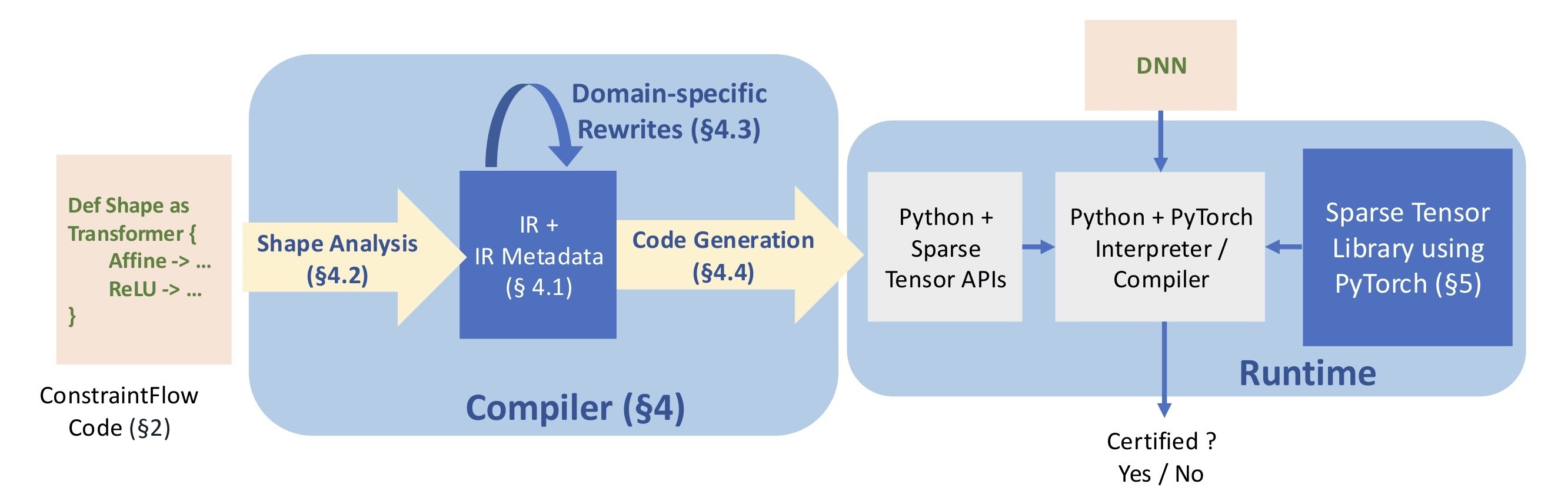
Neuton
Neuton is a compiler and execution framework for ConstraintFlow specifications. It translates high-level declarative certifier specifications into efficient executable implementations, bridging the gap between formally specified analyses and practical large-scale neural network verification.
AI for Formal Methods
This line of work focuses on using machine learning and program synthesis techniques to automate and scale formal methods. My goal is to use AI to generate, improve, and adapt formal analysis tools, optimizations, and reasoning procedures, reducing the manual effort required to design, implement, and maintain verification and analysis systems.
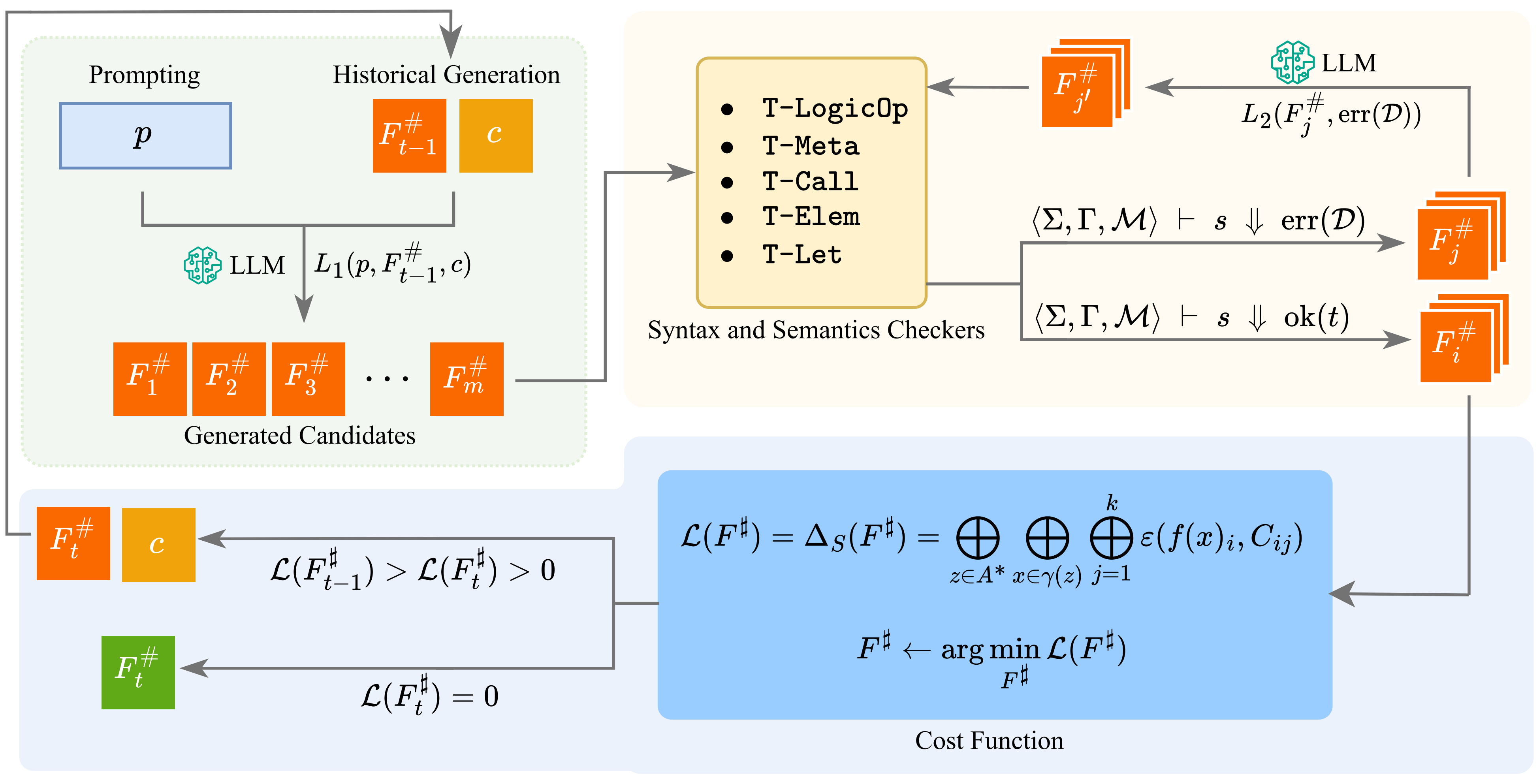
SAIL
SAIL automatically synthesizes new neural network certifiers by leveraging the ConstraintFlow DSL together with its soundness verifier and compiler. It explores the space of certifier designs and produces new certification procedures that are correct by construction.
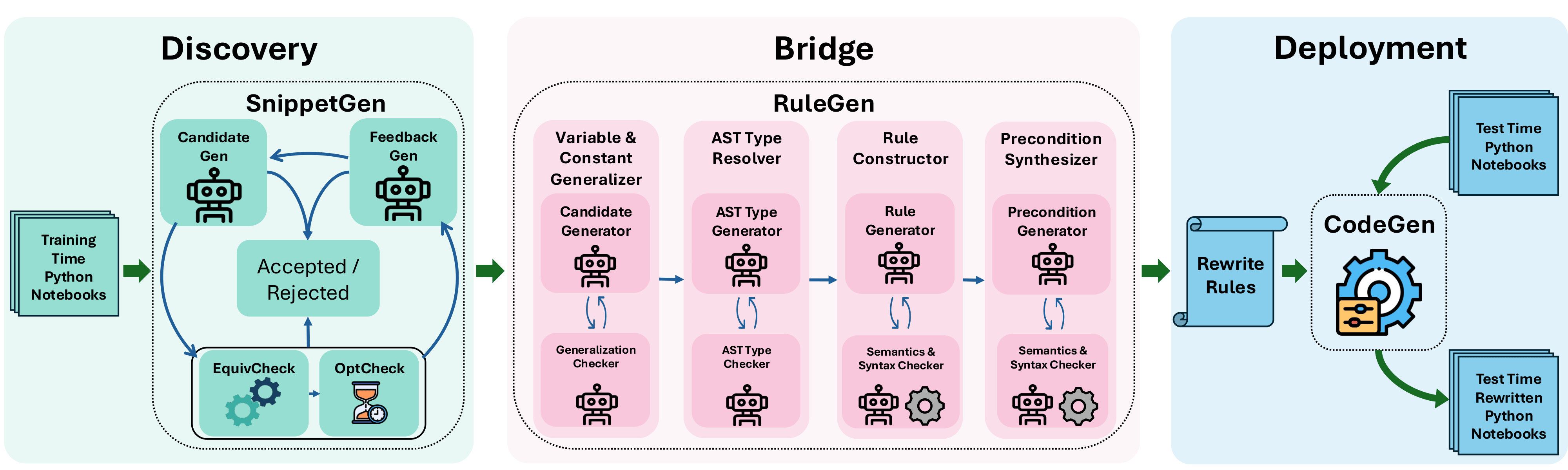
RuleFlow
RuleFlow automatically generates data-analysis and Pandas optimizations by combining large language models with compiler and program analysis techniques. It targets reusable, rule-based transformations that improve performance while preserving program semantics.
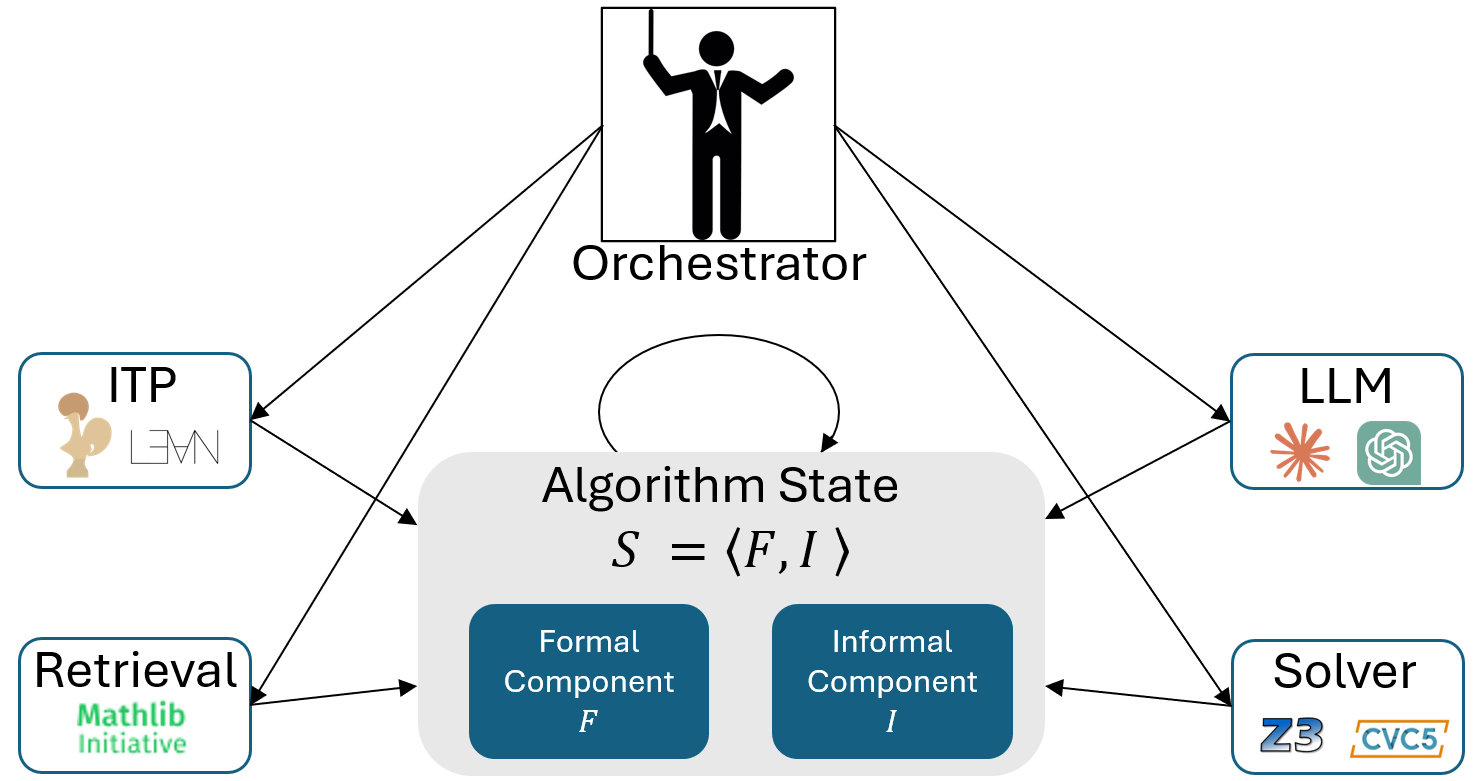
Automated Theorem Proving
This project studies the use of AI and large language models to assist and automate theorem proving. The goal is to support formal reasoning by guiding proof search, generating intermediate lemmas, and helping interact with modern theorem provers.